É comum na literatura termos os elementos da natureza, elementos básicos que constituem o mundo, representados por símbolos, cores e até mesmo espíritos. Em Frozen 2 acompanhamos Elza em uma nova aventura onde ela vê os elementos da natureza em forma de criaturas.
Um filósofo chamado Platão também via os elementos da natureza, mas não em forma de criaturas, ele via em forma de Poliedros. Você sabe o que são poliedros?
Um Poliedro é uma reunião de um número finito de polígonos planos.
Esses polígonos são chamados de faces do poliedro.
Em um poliedro é sempre possível “caminhar" pelas faces sem passar por nenhum vértice (cruzando apenas as arestas).
Os poliedros que iremos conhecer são chamados de Poliedros de Platão ou Poliedros regulares. Apesar de chamarmos assim, esses poliedros já existiam muito antes de Platão.
 |
| Escócia, cerca de 3000 a.C. |
Para um poliedro ser regular ele tem que
- ser convexo
- suas faces serem polígonos regulares iguais
- de cada vértice saem o mesmo número de arestas.
Platão nasceu em Atenas, hoje capital da Grécia, por volta de 428 a.C., e morreu no ano de 348 a.C. Foi um dos mais importantes filósofos grego e o grande responsável por divulgar os poliedros regulares que chamamos de Poliedros de Platão.
Platão começou a pensar que relação os poliedros regulares tinham com o mundo e assim encontrou para cada poliedros regulares um elemento da natureza.
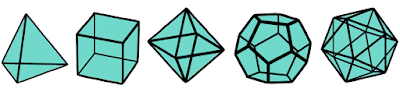
Existem apenas 5 poliedros regulares e vamos conhece-los agora!
O tetraedro possui 4 faces triangulares, 4 vértices e 6 arestas. Para Platão, o tetraedro representava o elemento fogo. Se observarmos, o tetraedro pode lembrar uma chama 🔥.
O cubro possui 6 faces quadradas, 8 vértices e 12 arestas. Para Platão, o cubo representava o elemento terra, pois era algo firme.
O octaedro possui 8 faces triangulares, 6 vértices e 12 arestas. Para Platão, o octaedro representava o elemento ar, pois parece que o octaedro está flutuando.
O icosaedro possui 20 faces triangulares, 12 vértices e 30 arestas. Para Platão, o icosaedro representava o elemento a água.
E por fim, temos o dodecaedro que possui 12 faces pentagonais, 20 vértices e 30 arestas. Para Platão, o dodecaedro representava o universo.

O Matemático Johannes Kepler era apaixonado por geometria e tentou usá-la para explicar a posição dos planetas no universo. Para isso, utilizou os Poliedros de Platão para separar os planetas.
O tetraedro para separar a esfera de Júpiter da de Marte;
O dodecaedro entre a esfera de Marte e a da Terra;
O icosaedro entre a esfera da Terra e a de Vénus;
O octaedro entre a esfera de Vénus e a da Mercúrio.
Devido a regularidade das faces, os poliedros de Platão são utilizados como dados em jogos de sorte, veja: