Desventuras em série, uma coleção de livros escrita por Daniel Handler, conta a história dos três irmãos Baudelaire que perderam seus pais em um incêndio e que passam por situações terríveis após ficarem órfãos.
Ao ler os livros você nota a ficção, pois seria impossível ter crianças tão azaradas ao ponto de absolutamente tudo terminar em algo trágico para elas. Mas vou te contar uma história real de um matemático brilhante que passou por situações tão extremas quanto a dos irmãos Baudelaire.
Mau começo - 1571
Johannes Kepler
Nossa história começa com uma bruxa. Bom, pelo menos para as pessoas daquela época a mãe de Johannes Kepler, Katharina Guldenmann, era considerada uma bruxa. Ela foi criada por sua tia que lhe ensinou sobre o mundo das ervas e curas, porém anos mais tarde sua tia foi queimada na fogueira acusada de bruxaria.
Ela casou-se com Heinrich Kepler e teve seis filhos, mas apenas três sobreviveram. Johannes Kepler foi um dos sobreviventes, porém nasceu prematuro e fraco. Nascer assim foi apenas o começo das desventuras de Kepler, pois ainda na infância teve varíola que deixou suas mãos aleijadas e prejudicou sua visão além de doenças de pele que nunca cicatrizavam.
Além das doenças, o dinheiro da família foi se esvaindo, o que levou Heinrich e Katharina a um relacionamento conturbado onde os dois possuíam um terrível mal-humor e Heinrich excedia no consumo de bebidas alcoólicas. Johannes Kepler chegou a descrever seu pai como “um homem cruel, condenado a um final ruim” e sua mãe como “fofoqueira e briguenta”.
Quando o dinheiro da família acabou Heinrich abandonou esposa e filhos o que levou a Katharina a se sustentar vendendo misturas de ervas para doenças comuns que os vizinhos diziam ser melhoradas com feitiços.
Kepler teve uma infância complicada com problemas de saúde, familiares e financeiros. Muitos nessas condições acabam se tornando adultos com sérios problemas emocionais. Porém, no escuro da noite Kepler encontrou um refúgio para sua dor.
Descobrindo o céu
Aos seis anos de idade Kepler observou com sua mãe o Grande Cometa de 1577 no céu noturno. Anos mais tarde viu seu primeiro eclipse lunar onde a lua "parecia bastante vermelha".
O Grande Cometa de 1577 sobre Praga
Kepler era excelente em matemática e adorava observar o céu. Ele também escrevia histórias de ficção cientifica sobre viagens a Lua e em uma de suas histórias, Somnium, há uma personagem sábia, mãe do personagem principal, que vende encantamentos mágicos e se comunica com um demônio (personagem bem semelhante com alguém desse post, não acha?).
Em uma escola local iniciou seus estudos. Mas foi na Universidade de Tübingen que frequentou um curso de matemática onde provou ser um matemático excepcional o que lhe proporcionou uma posição de professor de matemática, ainda com 23 anos de idade.
Ainda em Tübingen estudou astronomia com Michael Mästlin, um dos principais astrônomos. Naquela época eram conhecidos apenas seis planetas: Mercúrio, Vênus, Terra, Marte, Júpiter e Saturno.
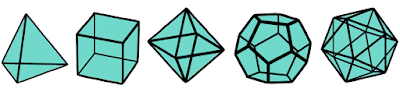
Assim como Hipátia de Alexandria, Kepler era apaixonado por geometria e tentou usá-la para explicar a posição dos planetas no universo. Para isso, utilizou os Poliedros de Platão para separar os planetas.
 |
Poliedros de Platão |
- O cubo para separar a esfera de Saturno da de Júpiter;
- O tetraedro para separar a esfera de Júpiter da de Marte;
- O dodecaedro entre a esfera de Marte e a da Terra;
- O icosaedro entre a esfera da Terra e a de Vénus;
- O octaedro entre a esfera de Vénus e a da Mercúrio.
Ele apresentou esse modelo no seu livro Mysterium, em 1596.
Foi assistente de Tycho Brahe, um astrônomo cuja morte foi relatada por Kepler que conta sobre um banquete que eles estavam e Brahe se recusou a deixar a mesa para se aliviar, pois não considerava uma atitude educada. Quando Brahe voltou para casa, ele não conseguia urinar e morreu 11 dias depois. Contam que Brahe perto de seu fim escreveu seu próprio epitáfio "Ele viveu como um sábio e morreu como um tolo”.
Após a morte de Brahe, Kepler assumiu seu lugar onde ganhou fama de louco dos signos, digo, astrólogo. Trabalhou para o imperador e uma de suas funções principais era fazer horóscopos, mas não era algo que o agradava.
Casamento
Para muitos o casamento costuma ser um momento de alegria e união. Barbara, já viuva de dois casamentos, queria se casar com Kepler, porém seus pais não aceitavam o casamento por conta das condições financeiras dele. Porém em 1597 os dois se casaram. Após casar, Barbara deu a luz a dois filhos que morreram na infância. Em 1602 nasceu uma menina seguida de dois meninos em 1604 e 1607. Seus filhos contraíram varíola e um deles morreu. Como se não bastasse, Barbara morreu um tempo depois.
Kepler não desistiu de ter um relacionamento amoroso e em 1613 casou-se com Susanna com quem teve seis filhos (três morreram na infância). Segundo Howard Eves, "o seu segundo casamento não foi mais feliz do que o primeiro, ainda que ele tenha analisado com precaução os méritos e deméritos de onze raparigas, antes de escolher a errada”.
Caça às bruxas
A Europa estava no auge da caça às bruxas e qualquer boato era perigoso e poderia colocar a vida de uma mulher em perigo. Foi o que aconteceu com a mãe de Kepler. Uma vizinha acusou Katharina de ter envenenado ela com uma de suas poções.
O procedimento para julgar se uma mulher era realmente uma bruxa envolvia torturas que poderiam resultar em morte. Essa situação levou Kepler a deixar de lado por um tempo suas pesquisas para defender sua mãe.
Lembra que Kepler escreveu que Katharina era uma mulher briguenta? Pois então, Katharina resolveu confrontar seus acusadores o que não deu muito certo, pois ela foi presa acusada de prática de bruxaria.
Kepler montou com seus advogados uma defesa com mais de 100 páginas destruindo os argumentos da promotoria que garantiu a absolvição de Katharina que não conseguiu aproveitar sua liberdade, pois morreu no ano seguinte.
O fim
Kepler descobriu que as órbitas planetárias não eram círculos, mas sim elipses. Então, descreveu o movimento planetário por três leis conhecidas como “Leis de Kepler".
Seu fim chegou cedo após adoecer aos 58 anos, tempo suficiente para que sua mente brilhante fosse reconhecida e admirada. Apesar das dificuldades que enfrentou desde a infância, Kepler nunca desistiu de estudar e desvendar os mistérios do universo.
Você conhece alguém que também passou por problemas na infância e que se tornou uma pessoa admirável? Compartilhe essa história com ela!